戞1復 彉榑
暵嵔揑側撪榩堟偼丄崅擹搙偺晧壸丒挿偄懾棷帪娫丒斾妑揑戝偒側悈懱愊丒榩撪偱偺撪晹惗嶻惈偺崅偝側偳偵傛傝摿挜晅偗傜傟丄峔憿揑偵墭戺偑恑峴偟傗偡偄偲偄偆摿挜傪帩偮丅
擔杮偺撪榩堟傪椺偵庢傞偲丄偦偺娐嫬栤戣傊偺庢傝慻傒偼丄岞奞懳嶔丒娐嫬暅尦乮憂憿乯丒惗懺宯偲偺嫟懚偲偄偭偨僉乕儚乕僪傪幉偵曄壔偟偰偒偰偄傞丅偦偟偰丄尰嵼偱偼丄娐嫬栤戣偺峀堟揑丒挿婜揑側帇栰偵棫偭偨昡壙傗懳嶔傪峫偊傞傋偒帪婜偵棃偰偄傞偲擣幆偝傟偰偄傞丅偙傟偑娐嫬栤戣偺儅僋儘壔偱偁傞丅傑偨丄惗暔稇詫n偵攝椂偡傞偨傔偵偼丄嬊強揑丒抁婜揑側乮旕掕忢揑側乯尰徾傪攃埇丒昡壙偡傞偙偲傕廳梫偱偁傝丄偙傟偼娐嫬栤戣偺儈僋儘壔偲偟偰曔傜偊傜傟偰偄傞丅
偦偆偟偨儈僋儘壔偝傟偨娐嫬栤戣傪峫偊傞偨傔偵偼丄偦偺僣乕儖偲偟偰娐嫬僔儈儏儗乕僔儑儞庤朄傪惍旛偡傞昁梫偑偁傞丅杮尋媶偼丄偙偆偟偨僔儈儏儗乕僔儑儞庤朄偺拞偱丄摿偵旝嵶側抧宍忦審傪峫椂偱偒丄嬊強棳傟傊偺揔梡惈偑崅偄偲峫偊傜傟傞乽棧嶶塓朄乿傪庢傝忋偘偨丅偙偺棧嶶塓朄傪娤應抣傗幚尡抣偵傛傞屄暿偺僷儔儊乕僞挷惍傪偡傞偙偲側偔丆幚嵺偺増娸堟偺棳傟偵揔梡偟丆偦偺梊應傪壜擻偵偡傞偙偲傪栚揑偲偟偨丅
戞俀復 棎棳儌僨儖偵傛傞棳傟夝愅偲棧嶶塓朄偺掕幃壔
塓棳傟偺寁嶼庤朄偲偦偺墳梡偲偟偰丄棧嶶塓朄偑NS曽掱幃偺捈愙夝朄偲偟偰敪揥偟偰偒偨宱堒偲丄偦偺掕幃壔傪帵偟丄棧嶶塓朄偺摿挜偲婎杮揑峫偊曽傪夝愢偡傞偲偲傕偵丄棳懍応偺媮傔曽丄埑椡応偺媮傔曽偵偮偄偰惍棟偟偨丅
摿偵丄杮庤朄偺摿挜偱偁傞奼嶶塓乮棧嶶塓乯偺儌僨儖壔偵偮偄偰丄偦偺棟榑揑幚尡揑崻嫆傪帵偟丄塓拞怱偐傜偺嫍棧![]() 偵偍偗傞愙慄棳懍
偵偍偗傞愙慄棳懍![]() 傪
傪
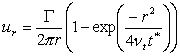
乮侾乯
偺宍偱梌偊傞偙偲偱丅懡悢偺塓揰偺廤崌傪1偮偺棧嶶塓偱戙昞偝偣丄岠棪揑側寁嶼傪峴偆偙偲偑偱偒傞壜擻惈傪帵偟偨丅偙偙偵丄![]() 偼弞娐丄
偼弞娐丄![]() 偼奼嶶偺戝偒偝偺僷儔儊乕僞丄
偼奼嶶偺戝偒偝偺僷儔儊乕僞丄![]() 偼塓曻弌屻偺宱夁帪娫偱偁傞丅埲壓偺復偵偍偄偰丄條乆側寁嶼働乕僗偵偍偄偰屄暿偵揔梡惈傪敾掕偟側偑傜丄偙偺掕幃壔偺懨摉惈偵偮偄偰専摙偟偰偄偔
偼塓曻弌屻偺宱夁帪娫偱偁傞丅埲壓偺復偵偍偄偰丄條乆側寁嶼働乕僗偵偍偄偰屄暿偵揔梡惈傪敾掕偟側偑傜丄偙偺掕幃壔偺懨摉惈偵偮偄偰専摙偟偰偄偔
戞俁復 婎慴悈棟尰徾偺嵞尰
傑偢丄幚尡悈楬偵偍偄偰惗偠傞婯柾偺棳傟偁傞偄偼尰抧偱偺彫婯柾側棳傟傪専摙偺懳徾偲偟偰丄偙傟傪棧嶶塓朄偵傛傝嵞尰偡傞偙偲傪帋傒偨丅偙偙偱偼丄偙偺庤朄傪傛傝堦斒揑側棳傟偵揔梡偡傞忋偱昁梫偲側傞儌僨儖僷儔儊乕僞偺嬶懱揑側掕幃壔偵偮偄偰柧傜偐偵偟偨丅
偦傟偧傟偺専摙偼丄悈棟柾宆幚尡傗尰抧娤應偵傛傞棳傟応偺摿挜偺攃埇偲丄偦偺棳傟傪棧嶶塓朄偵傛偭偰嵞尰偡傞偙偲偵傛傝峴傢傟丄棧嶶塓朄偵偍偗傞嫬奅忦審偺梌偊曽丄婎杮揑側僷儔儊乕僞偺愝掕曽朄偵偮偄偰峫嶡偟偨丅
傑偢丄扨堦暵嫬奅偺忦審偲偟偰丄堦條側棳傟偵懳偟偰妏搙傪帩偭偰偍偐傟偨暯斅攚屻偵敪惗偡傞塓楍傪庢傝忋偘偨乮恾亅侾乯丅偙傟偵傛傝丄暯斅傪庢傝埻傓暵嬋慄忋偵攝抲偝傟偨棧嶶塓偵傛傝暵嫬奅傪愝掕偡傞曽朄偲丄偦偺攳棧揰偵埵抲偡傞棧嶶塓偺曻弌偵傛傞攳棧塓偺嵞尰曽朄偵娭偡傞婎慴揑側専摙傪峴偭偨丅摿偵丄偦偺敪惗偡傞塓楍偺僷僞乕儞偺嵞尰偵拝栚偟丄揔摉側嫬奅梫慺偺攝抲枾搙傗丄棧嶶塓偲偟偰棳傟応偵曻弌偝傟偨塓偺徚挿傪寛傔傞僷儔儊乕僞偺梌偊曽偵偮偄偰偺巜恓傪摼偨丅
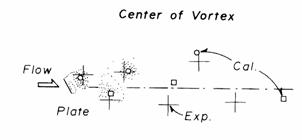
恾亅侾丗幬傔暯斅攚屻偺塓楍
師偵丄扨堦奐嫬奅偺忦審偲偟偰丄嶸慹搙偺撌晹廃曈偺棳傟傪庢傝忋偘偨丅偙傟偵傛傝丄撌晹廃曈偺嫬奅忦審傪侾杮偺慄嫬奅偵傛傝嵞尰偡傞奐嫬奅偺愝掕曽朄偲丄堦扷攳棧偟偨塓偲懠偺棧嶶塓偲偺姳徛偵娭偡傞専摙傪峴偭偨丅摿偵丄嶸慹搙偺戝偒偝偲嬻娫攝抲偲塓姳徛偺娭楢傪拝栚偟丄奐嫬奅傪扨弮側侾楍偺棧嶶塓偱梌偊傞偙偲偺懨摉惈偑専徹偝傟丄棧嶶塓偺曻弌曽岦側偳偑椙岲偵嵞尰偝傟傞偙偲傪妋擣偟偨丅
嵟屻偵丄暋悢暵嫬奅偺忦審偲偟偰丄堦條側棳傟偵抲偐傟偨懡悢偺墌拰楍廃曈偺棳傟傪庢傝忋偘偨丅偙傟偵傛傝丄懡悢偺屒棫嫬奅偑懚嵼偡傞応崌偺嫬奅偺愝掕曽朄偵偮偄偰専摙偟偨丅摿偵丄墌拰楍傪捠夁偡傞嵺偵敪惗偡傞懾棷堟傗暚棳忬偺棳傟偺僷僞乕儞丄墌拰楍孮懱偲偟偰偺掞峈學悢側偳偵拝栚偟丄暋悢嫬奅偺憡屳姳徛儌僨儖傪梡偄偨嵞尰寁嶼偺懨摉惈傪専徹偟偨寢壥丄尒偐偗偺掞峈學悢偺尭彮側偳偑嵞尰偝傟傞偙偲側偳偑妋擣偝傟丄棧嶶塓朄偵傛傞暋悢暵嫬奅偺寁嶼朄偑専徹偝傟偨丅
戞係復 増娸堟棳傟偺夝愅乮侾乯 -抧宍惈偺攳棧塓-
杮復偱偼丄尦棃僫價僄丒僗僩乕僋僗曽掱幃偺捈愙夝朄偲偟偰埵抲晅偗傜傟偰偒偨棧嶶塓朄傪丄棎棳儌僨儖偲偟偰埵抲晅偗丄増娸堟偺棳傟偵揔梡偱偒傞傛偆偵奼挘偟偨丅
傑偢丄暯柺擇師尦偺寁嶼庤朄偱偁傞棧嶶塓朄偑揔摉側曽朄偱弨嶰師尦揑側増娸堟摿桳偺忦審乮掙柺杸嶤偵傛傞塭嬁摍乯傪庢傝崬傓偙偲偑壜擻偱偁傞偙偲傪丄嫮偄挭棳偺拞偵屒棫偟偰懚嵼偡傞Rattary搰廃曈偺旕懳徧側屻棳塓偺僷僞乕儞偵偮偄偰専摙偡傞偙偲偱帵偟偨乮恾亅俀乯丅
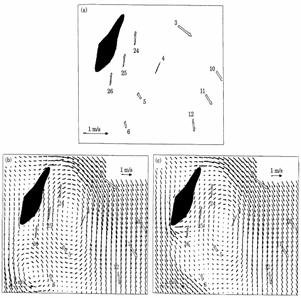
恾亅俀丗Rattary搰廃曈偺棳傟丅(a) 娤應抣丄(b) 棧嶶塓朄偵傛傞嵞尰乮掙柺杸嶤偵傛傞塭嬁傪峫椂偟側偄忦審偱偺寁嶼寢壥乯丄(c)
棧嶶塓朄偵傛傞嵞尰乮掙柺杸嶤偵傛傞塭嬁傪峫椂偡傞忦審偱偺寁嶼寢壥乯丅
傑偨丄挭棳偲僿僢僪儔儞僪偺姳徛偵傛傞悈夠峔憿偺宍惉夁掱傪専摙偟丄奀娸慄偲偄偆楢懕嫬奅嬤曈偱偺塓峔憿偺寁嶼偑壜擻偱偁傞偙偲傪帵偟丄塓棳偵傛傞僩儔僢僾岠壥偑僷僢僠忬偺崅墫暘悈偲掅墫暘悈偺暘晍傪宍惉偡傞壜擻惈傪帵偡偙偲偑偱偒偨丅
戞俆復 増娸堟棳傟偺夝愅乮俀乯 -奀嫭晹偺棳傟-
杮復偱偼丄増娸堟偵偍偄偰摿挜揑偱偁傞撪晹棳傟偺栤戣偵棧嶶塓朄傪揔梡偡傞偨傔偵丄奀嫭晹偺傛偆偵椉娸偐傜偺攳棧塓偑姳徛偟崌偆傛偆側応偱専徹傪峴偭偨丅
傑偢丄彫偝側奐岥晹傪巆偟偰奀堟傪埻偄崬傒丄偙偺奐岥晹傪捠偟偰偺挭幀偵傛傞奀悈岎姺夁掱傪棙梡偟偨憿棳掔偱偁傞乽僌僠幃憿棳掔乿偵傛傞憿棳岠壥偵偮偄偰丄條乆側僗働乕儖偺幚尡傪峴偄丄偦偺寢壥偲偺斾妑傪捠偠偰杮寁嶼朄傪娷傓庬乆偺寁嶼朄偵傛傞嵞尰寁嶼偺惛搙専徹傪峴偭偨丅僌僠幃憿棳掔偺奐岥棪偑彫偝偔側傞偲丄奐岥晹晅嬤偱偺棳懍偑戝偒偔側傝嶰師尦惈偑嫮傑傞丅偙傟傪廬棃偺尩枾側嶰師尦寁嶼庤朄偵傛傝梊應偡傞側傜偽椙岲側堦抳傪尒偣傞堦曽偱丄媅帡嶰師尦寁嶼朄偱偁傞3D-ADI偵傛傟偽丄偦偺梊應寢壥偼悈棟柾宆幚尡偵傛傝摼傜傟傞傕偺偲孹岦傪堎偵偡傞偙偲偑巜揈偝傟偰偄傞丅棧嶶塓朄偼丄懠偺嶰師尦寁嶼朄偵斾傋偰偒傢傔偰娙曋偱偁傝側偑傜丄偦偺夝愅惛搙偼忋婰擇偮偺庤朄偺拞娫偵埵抲偡傞偙偲偑妋擣偝傟偨丅偙傟偼丄悈暯揑側嬻娫暘夝擻偑崅偄偙偲偵傛傝丄奐岥晹偵偍偗傞攳棧塓偺惗惉夁掱傪惛搙椙偔嵞尰偱偒偰偄傞偙偲偺惉壥偱偁傞偲峫偊傜傟偨丅
師偵丄儊僜僗働乕儖偺塓棳摦傊偺揔梡惈傪専摙偡傞偨傔偵丄悢昐倣婯柾偺搰(偙偙偱偼Palm彅搰)偺娫偵偁傞奀嫭晹偺棳傟傗丄悢倠倣婯柾偺搶嫗榩榩岥晹偵偍偗傞棳傟傪専摙偺懳徾偲偟偨乮恾亅俁乯丅偙偙偱偼丄尰抧僗働乕儖偱偺塓傪懆偊傞偨傔偵丄廬棃偐傜峴傢傟偰偒偨棳懍寁偺學棷傗丄塯峲幃挻壒攇棳懍寁偵傛傞娤應偵壛偊丄暯柺揑偵昞柺棳懍傪娤應偱偒傞奀梞抁攇儗乕僟傪棙梡偟偨尰抧娤應傪峴偭偰偍傝丄偦偺寢壥傪摜傑偊偰尰徾偺徻嵶偵偮偄偰榑偠偨丅傑偨丄偙偺尰徾偵杮榑暥偱奐敪偟偰偒偨夝愅庤朄傪揔梡偡傞偙偲傕帋傒偰偍傝丄寢壥偲偟偰丄娤應偵傛偭偰妋擣偝傟偨嬻娫揑側塓峔憿偑悢抣寁嶼偵傛偭偰傕嵞尰偝傟傞偙偲傪帵偟偨丅側偍丄桳尷梫慺朄側偳偺嬻娫揑偵崅偄暘夝擻傪傕偮偲偝傟傞寁嶼庤朄傪梡偄偰傕丄塓偺婯柾傗曄宍偑昁偢偟傕偆傑偔嵞尰偝傟側偄偺偵懳偟偰丄棧嶶塓朄傪梡偄傞偲丄挭棳傪奜晹棳傟偲偟偰墲暅棳偱嬤帡偡傞偙偲傗丄嫬奅傪1楍偺嫬奅塓揰楍偱嬤帡偡傞偙偲偵傛傝丄斾妑揑寁嶼晧壸傪偐偗偢偵丄奀嫭晹廃曈偺暚棳峔憿偺帪娫揑曄壔傗丄懾棷堟偺嬻娫婯柾側偳傪嵞尰壜擻偱偁傞偙偲偑傢偐偭偨丅埲忋偺傛偆杮尋媶偱専摙偟偰偒偨夝愅庤朄傪梡偄傞偙偲偱丄増娸堟偵偍偗傞棳傟偺僷僞乕儞傗悈夠峔憿偺宍惉夁掱丄奀悈岎姺婡峔側偳傪娙曋偐偮斾妑揑惛搙傛偔梊應偱偒傞偙偲偑帵偝傟偨丅
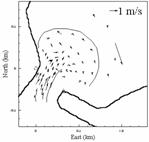
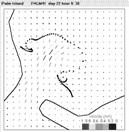
恾亅俁丗Palm彅搰偺奀嫭晹偺棳傟丅嵍偼VHF儗乕僟偵傛傞娤應抣丄塃偑棧嶶塓朄偵傛傞寁嶼抣丅
戞俇復 寢榑
杮榑暥偱偼丄棧嶶塓朄偵偍偗傞僷儔儊乕僞偺摑堦揑側寛掕曽朄傪採埬偟丄條乆側忦審壓偺棳傟傪懳徾偲偟偰棧嶶塓朄偵傛傞寁嶼傪峴偄丄偙傟傜傪悈棟柾宆幚尡傗尰抧娤應偺寢壥偲斾妑偡傞偙偲偱丄偦偺揔梡惈偑峀偄偙偲傪幚徹揑偵徹柧偟偨乮儗僀僲儖僘悢偱1000乣80000乯丅傑偨丄儗僀僲儖僘悢偺揔梡斖埻偩偗偱側偔丄堎側傞悈夠峔憿傪偲傞條乆側栤戣偵懳偟偰偺揔梡偑壜擻偱偁傞偙偲偑帵嵈偝傟偨丅偟偐偟丄増娸晹偺棳傟偵偙偺曽朄傪揔梡偡傞嵺偵偼丄偦偺娙曋惈偲堷偒姺偊偵丄乮侾乯塓偺擲惈奼嶶偵懳偟偰悈怺偺曄壔偺岠壥偑庢傝擖傟傜傟偰偄側偄偙偲乮俀乯応偺棳傟偲偟偰梌偊傞億僥儞僔儍儖棳偵丄掙柺偣傫抐椡偺塭嬁偑擖傜側偄偙偲乮俁乯墫暘傗悈壏摍偺堘偄偵傛傞枾搙岠壥傪寁嶼偱偒側偄偙偲側偳寁嶼朄偺尷奅偑偁傞丅
偙偆偟偨丄寁嶼朄偺挿強丒抁強傪廫暘偵棟夝偟偨忋偱梡偄傞側傜偽丄偙偺棧嶶塓朄偼増娸堟偵偍偗傞旝嵶側棳傟偺寁嶼庤朄偲偟偰桳梡偱偁傞偲尵偊丄嬻娫揑丒帪娫揑側曄摦僗働乕儖傪挻偊偰増娸堟棳傟傪専摙偡傞寁嶼偺僣乕儖偺傂偲偮偲偟偰偺崱屻偺峏側傞妶梡偑婜懸偝傟傞丅
幱帿
杮榑暥偼丆棟岺妛晹幮夛娐嫬岺妛壢娭崻惓恖嫵庼丆麮愳搊嫵庼丆婡夿岺妛壢懢揷桳嫵庼偺偛巜摫傪摼偰偲傝傑偲傔傜傟傑偟偨丏婰偟偰姶幱偄偨偟傑偡丏